题型
很简洁,只有3道编程题。都不难
具体题目
1. 一个存在环的链表,寻找环的入口。
力扣原题,写过就不难的。链接在这
使用快慢指针来解题。快指针一次走两步,慢指针一次走一步。当两指针相遇时停下。
设慢指针走过的节点数为a,那么快指针走过的节点数就是2a。
链表未成环的节点数为x,成环的节点数为y。
两指针相遇位置离环起点的节点数为z。
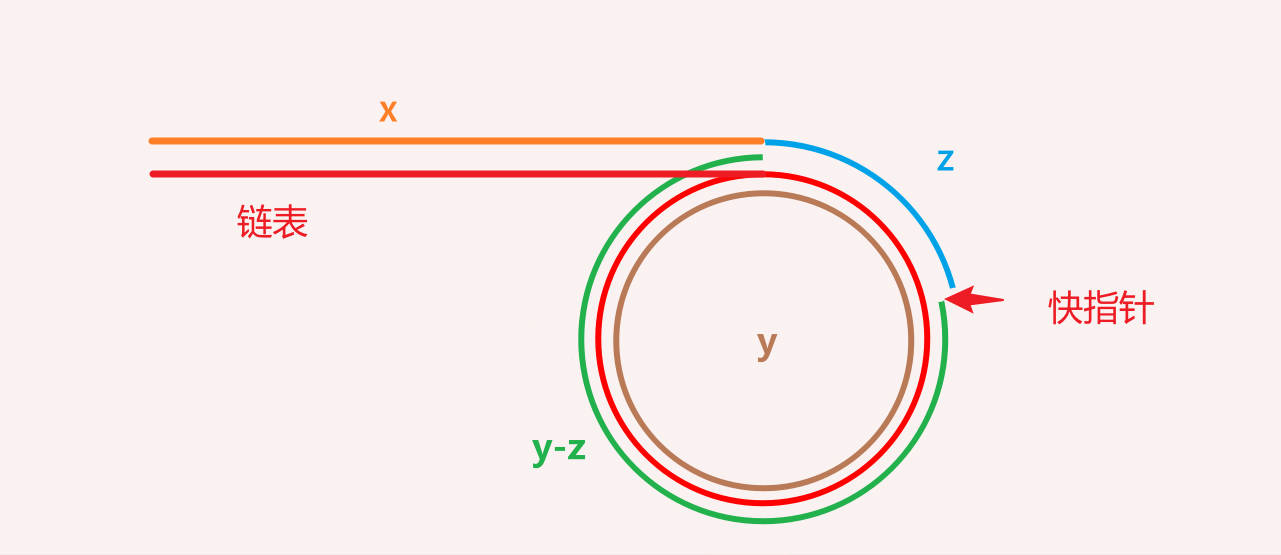
如果快指针从此刻开始一次只走一个节点,走完(n-1)y + (y-z)个节点之后,就到了环的起点。
又因为x = (n-1)y + (y-z),所以,我们可以将慢指针放到链表开头,和快指针一起走。当两个指针相遇时,就是走到了环的起点。
分析完成,具体代码如下:
/**
* Definition for singly-linked list.
* public class ListNode {
* public int val;
* public ListNode next;
* public ListNode(int x) {
* val = x;
* next = null;
* }
* }
*/
public class Solution {
public ListNode DetectCycle(ListNode head)
{
if(head == null || head.next == null) return null;
ListNode slow = head;
ListNode fast = head;
do
{
slow = slow.next;
if (fast != null && fast.next != null)
fast = fast.next.next;
else
return null;
} while (slow != fast);
//循环结束时,两者相遇
slow = head;
while(slow != fast)
{
slow = slow.next;
fast = fast.next;
}
return fast;
}
}
2. 给定若干个攻击范围,求玩家最少移动几步才能避开攻击。
具体题目:
在一张25*25的地图上(具体忘记是多大的了)
有两种类型的攻击范围,一种是矩形,一种是圆形。
矩形攻击输入矩形左上角和右下角的坐标。圆形攻击输入圆心的坐标和半径。
某一格子任何一部分和攻击范围重叠时,该格子都算作在攻击范围内。
玩家只能上下左右移动,请输出玩家最少走几步才能脱离攻击范围。
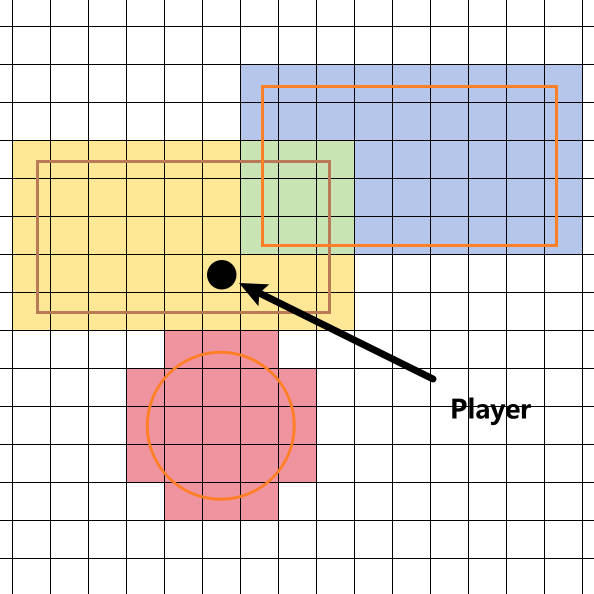
输入示例:
5 8 (玩家坐标)
3 (攻击的数量)
0.6 12.4 8.3 7.4 (矩形攻击的左上角和右下角坐标)
6.6 14.4 14.2 10.2
-1 5.5 4.5 1.8 (-1表示圆形攻击,然后是圆心坐标和攻击半径)
这题很明显的BFS,但是麻烦的是要处理攻击范围。尤其是圆形的。
首先先来看怎么处理攻击范围。
- 将每个格子的坐标认为是每个格子左下角的点的坐标。不这么做的话格子的坐标实际都是
.5的。与网格坐标冲突。
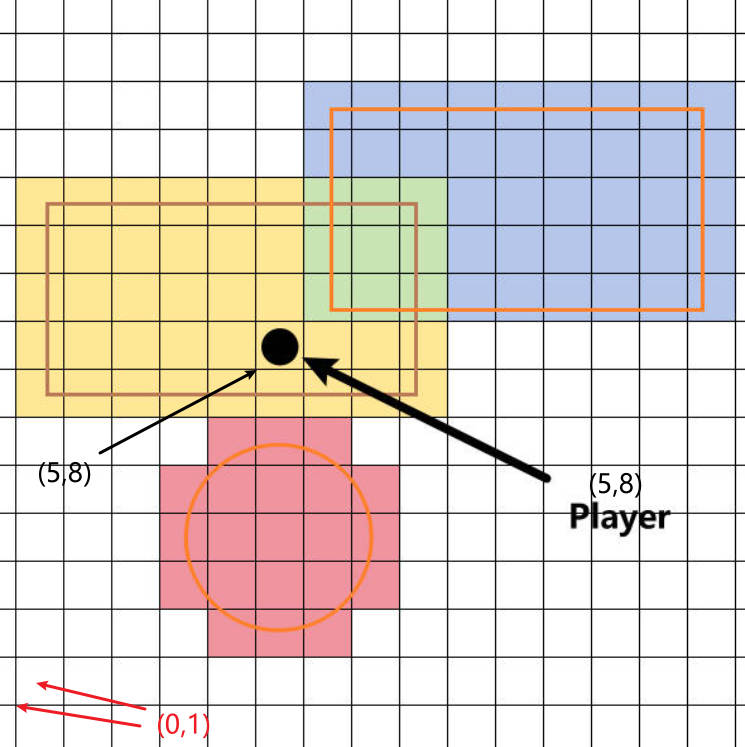
- 矩形攻击范围,左,下边界要向下取整,右,上边界要向上取整。也就是会变成涂色的范围。
- 圆形攻击范围,需要在设置地图时处理。
为了方便BFS,我们应当用二维数组创建一张地图,将攻击范围反映到地图上。
使用bool[,]来标记格子是否在攻击范围内。
矩形攻击范围很好处理,因为已经将攻击范围处理好了,直接遍历就行。
圆形攻击范围较为麻烦。我的处理方法如下:
- 首先遍历图示范围,用圆心坐标和半径可以轻松计算出该范围。
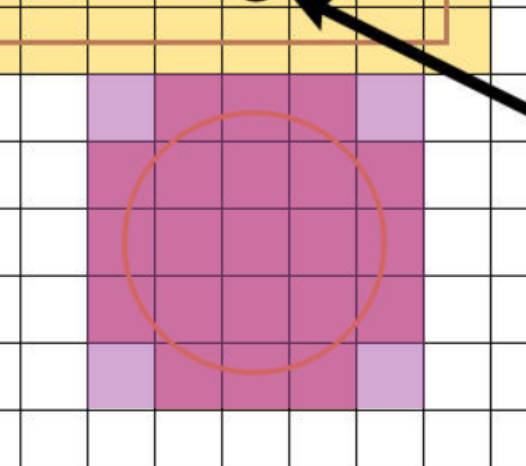
- 可以发现,当某个网格点在圆形攻击范围内时,其周围4个格子都是攻击范围。遍历这些网格点,若网格点到圆心的距离小于半径,则将其周围4个格子都标记成攻击范围。
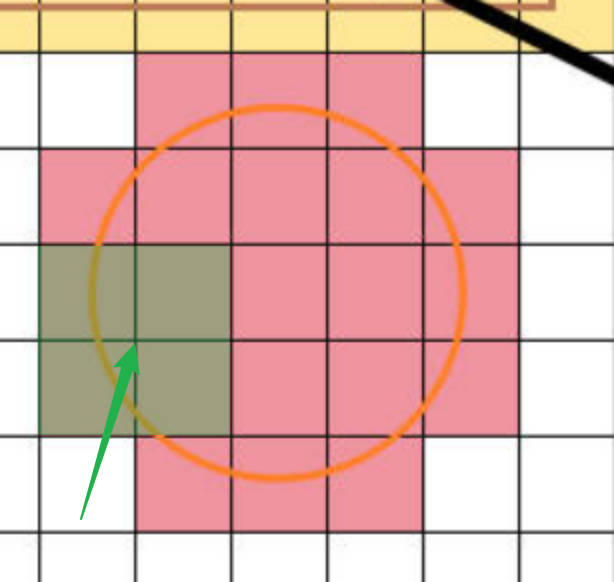
攻击范围处理完成,接下来就只是简单的BFS环节了。
完整代码如下:
public static void Main() {
Solution solution = new Solution();
string line = "";
//读取玩家坐标
(int, int) playerPos;
line = Console.ReadLine();
string[] tokens = line.Split(' ');
playerPos.Item1 = int.Parse(tokens[0]);
playerPos.Item2 = int.Parse(tokens[1]);
//读取攻击范围数量
line = Console.ReadLine();
tokens = line.Split(' ');
int enterCount = int.Parse(tokens[0]);
//读取攻击范围
List<List<float>> attackList = new List<List<float>>(enterCount);
while (enterCount-- > 0) {
line = Console.ReadLine();
tokens = line.Split(' ');
attackList.Add(new List<float>(4) {
float.Parse(tokens[0]),
float.Parse(tokens[1]),
float.Parse(tokens[2]),
float.Parse(tokens[3])
});
}
//创建地图
bool[,] map = new bool[25, 25];
for (int i = 0; i < attackList.Count; i++) {
//第一个参数大于0时,说明是矩形攻击
if (attackList[i][0] > 0) {
//调整矩形攻击范围
attackList[i][0] = (int)Math.Floor(attackList[i][0]);
attackList[i][1] = (int)Math.Ceiling(attackList[i][1]);
attackList[i][2] = (int)Math.Ceiling(attackList[i][2]);
attackList[i][3] = (int)Math.Floor(attackList[i][3]);
//将攻击范围内的格子设置为true
for (int j = (int)attackList[i][0]; j < attackList[i][2]; j++) {
for (int k = (int)attackList[i][3]; k < attackList[i][1]; k++) {
map[j, k] = true;
}
}
} else {
//第一个参数小于0,说明是圆形攻击
float centerX = attackList[i][1];
float centerY = attackList[i][2];
float r = attackList[i][3];
for (int j = (int)Math.Floor(centerX - r); j < (int)Math.Ceiling(centerX + r); j++) {
for (int k = (int)Math.Floor(centerY - r); k < (int)Math.Ceiling(centerY + r); k++) {
if (Math.Pow(j - centerX, 2) + Math.Pow(k - centerY, 2) < r * r) {
map[j, k] = true;
map[j - 1, k] = true;
map[j, k - 1] = true;
map[j - 1, k - 1] = true;
}
}
}
}
//BFS模板
Queue<(int, int)> queue = new Queue<(int, int)> ();
queue.Enqueue(playerPos);
int length = 0;
bool isEscap = false;
while(queue.Count > 0) {
int count = queue.Count;
while (count-- > 0) {
(int, int) tempPos = queue.Dequeue();
if (!map[tempPos.Item1, tempPos.Item2]) {
queue.Clear();
isEscap = true;
break;
} else {
queue.Enqueue((tempPos.Item1 - 1, tempPos.Item2));
queue.Enqueue((tempPos.Item1 + 1, tempPos.Item2));
queue.Enqueue((tempPos.Item1, tempPos.Item2 + 1));
queue.Enqueue((tempPos.Item1, tempPos.Item2 + 1));
}
}
if(!isEscap) length++;
}
Console.WriteLine(length);
Console.ReadKey();
}
}
3. 硬币兑换
具体题目:
给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。
计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。
你可以认为每种硬币的数量是无限的。
力扣原题,完全背包,求最少需要几个硬币。链接在这
很简单的题,但是笔试的时候没AC。。。
平时随便写的题,一笔试就写得稀烂。
代码如下:
public int CoinChange(int[] coins, int amount) {
int[] dp = new int[amount + 1];
for(int i = 1; i < dp.Length; i++){
dp[i] = int.MaxValue;
}
for(int i = 0; i < coins.Length; i++){
for(int j = coins[i]; j < dp.Length; j++){
if(dp[j - coins[i]] != int.MaxValue)
dp[j] = Math.Min(dp[j - coins[i]] + 1, dp[j]);
}
}
if(dp[dp.Length - 1] == int.MaxValue) return -1;
return dp[dp.Length - 1];
}
