目录
考前准备
在西山居的笔试之前,先经历了一次FunPlus的纯C++笔试,信心很受打击。再加上之前在牛客网上查过西山居的笔试,看见都是吐槽纯考C++的,在考试之前的心态已经摆烂了。。。在开始考试的时候完全是以`“让我看看这次的题目能有多难”`的看乐子心态去考的。实际上难度不高,考完很后悔为什么没有好好准备导致考试的时候浪费了不少时间。
所以网络上的笔经面经要看,但不要完全相信他人对于难度的描述,谁知道该公司下一次笔试还和之前一样呢?
试卷总体评价
和FunPlus比起来简单太多了!(可能只是单纯因为我C++水平太烂)考试分为3种题型
- 10道选择题
计网,计组,操作系统的内容不多,大概才2-3题,大部分是数据结构和看程序写结果。程序用C/C++写的,但是个人感觉难度偏低。(其实还是要对C++有一定了解才能写出来)
- 2道填空题
第一题考察的是排序内容,第二题考察的是概率论(比较简单的)
- 3道编程题
可以用C#! 只要是牛客网上能用的编程语言都可以用!具体难度我做不出评价,毕竟我只笔试过两家。
一个建议:
请一定把你所用的编程语言中常用的数据结构及其函数记清楚
具体题目
所有的题目我肯定是记不全的,只写一写我还记得的。
选择题
1. 一组元素入栈的顺序为abcdef,那么出栈的顺序不可能是?
很简单的题,就是把选项的出栈顺序一个个试一遍看看哪个不可能就好了。
比如
入 入 出 出 入 入 出 出 入 入 出 出那么出栈顺序就是badcfe但是我完全理解错题目了!以为
abcdef是连着入栈的,根据我浅薄的知识判断出栈顺序只有可能是fedcba,看完题目直接懵了。只好乱选了一个。
2. 有一个虚拟存储系统,若进程在内存中占3页(开始是内存为空),若采用先进先出(FIFO)页面淘汰算法,当执行如下访问页面序列后,会发生多少次缺页?
序列:1, 2, 3, 4, 5, 1, 2, 5, 1, 2, 3, 4, 5
内存大小为3,使用FIFO淘汰算法,开始内存为空。
前面五次由于都是第一次调用的页面,所以坑定会发生缺页,前5次调用完,缺页5次,内存中为
3, 4, 5再接下来2次,访问1和2,但是内存中已经不存在1,2了。也会发生缺页,缺页7次,内存中为
5, 1, 2再接下来访问
5, 1, 2,由于内存中存在5,1,2,不发生缺页。最后是`3, 4, 5’,会发生3次缺页,总计就是10次缺页。
3. 看程序写结果:
#include <iostream> using namespace std; void Fun1(int a){ a++; } void Fun2(int* a){ a++; } int main(){ int abc = 100, xyz = 13; Fun1(abc); abc = xyz; Fun2(&xyz); cout<<abc; return 0; }
C++
程序应该是这样,写的不一定对。反正就是考察指针的基础知识。如果我程序没写错答案就是13
4. 请问以下程序一共输出了几次”-“?
int main(){ for(int i = 0; i < 2; i++){ fork(); printf("-"); } return 0; }
C
fork()函数会创建和当前完全一样的子进程,也就是会把程序一分为二,同时这个fork函数还写在for循环里。也就是子进程还会被分割成2个子进程。
二叉树,嘿嘿,二叉树看起来就像一个满二叉树,问你一个深度为2的满二叉树有几个节点。(其实这题就2层根本不用这样理解)
如果我程序没写错,且我理解的没错的话,答案应该是7
选择题我就只记得上面这些了,不过接下来的题我差不多都记得。
填空题
1. adfbgce 要经过____次两两交换可以变成 abcdefg。任意顺序排列的abcdefg最少要____次两两交换才能还原,最多要____次。
这题其实我不会,排序的知识我没有!

第一个空应该就是3次
这题后两个空我没太读懂是什么意思,最少要几次两两交换?
abcdefg的话0次不用交换
交换排序最差的情况至少要6次
我不知道题目问的是上面的哪一种情况。
最多的话,应该是gfedcba然后冒泡排序吧) 那就是21次。
2. 两个骰子,同时掷出,两者之和为7的概率是____
有一种特殊的骰子,掷出6的概率是50%,掷出其他的概率都是10%,同时掷出,两者之和为7的概率是____
是简单的概率论,两个骰子相互独立
相加为7的情况有 1,6__2,5__3,4__4,3__5,2,__6,1 每种情况的概率是1/36。六种情况加起来就是1/6
第二空也一样,只不过带6的情况概率是1/20,其他情况概率是1/100,六种加起来就是7/50
编程题
编程题不能用IDE,但是可以用所有牛客网支持的语言。是核心代码模式,不是ACM。
1. 给定一组面试时间,每个面试时间分为开始时间和结束时间,每场面试需要2位面试官,面试官不需要休息,面试不可中断。请计算一共需要多少个面试官。
我个人的解法是将
开始时间和结束时间分别装进两个数组里再排序。应该可以用优先队列,但是我死活记不起来优先队列是怎么拼的。没有IDE我就是个纯废物
排序之后就很容易写了,以下是C#的核心代码
//面试官总数 int count = 0; //空闲的面试官 int freeNum = 0; while(startQueue.Count > 0){ if(startQueue.Peek() < endQueue.Peek()){ if(freeNum == 0) count += 2; else freeNum -= 2; startQueue.Dequeue(); }else{ while(startQueue.Peek() >= endQueue.Peek()){ freeNum += 2; endQueue.Dequeue(); } } }
C#
2. 在一张无限大的中国象棋的棋盘的(0,0)点有一只马,给一个目标点的坐标,求到达该目标点,马最少要走几步。
这题我没写出来,需要用BFS来写,但是考试的时候没时间了。
马有8种行走的方向
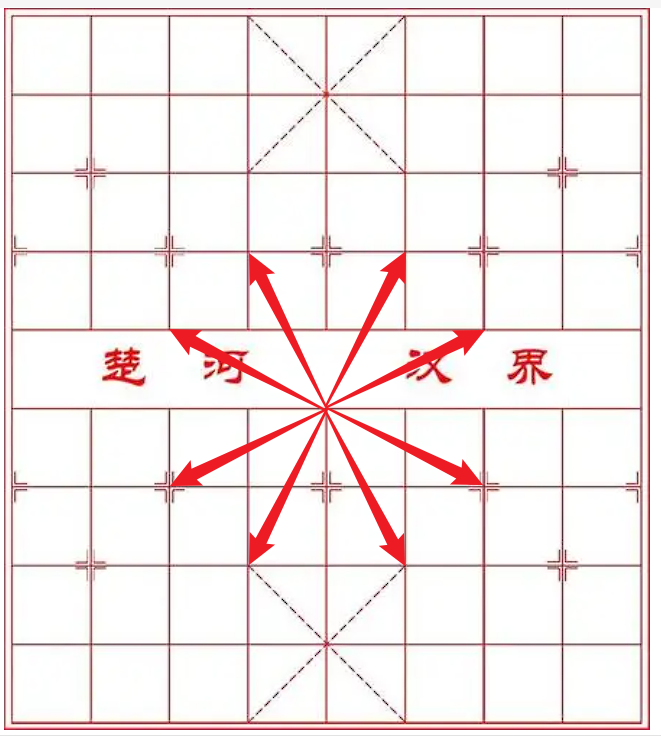
如果直接用广度优先搜索的话,每个目标又可以衍生出8个目标,那么时间和空间复杂度都将会是O(8^n)。
我不知道考试的时候直接广搜能不能过,但是我觉得还是要剪枝一下比较好。 我的剪枝思路如下:
1.以马当前位置为原点,将周围分成四个象限。以逆时针来算,保持左开右闭的原则。
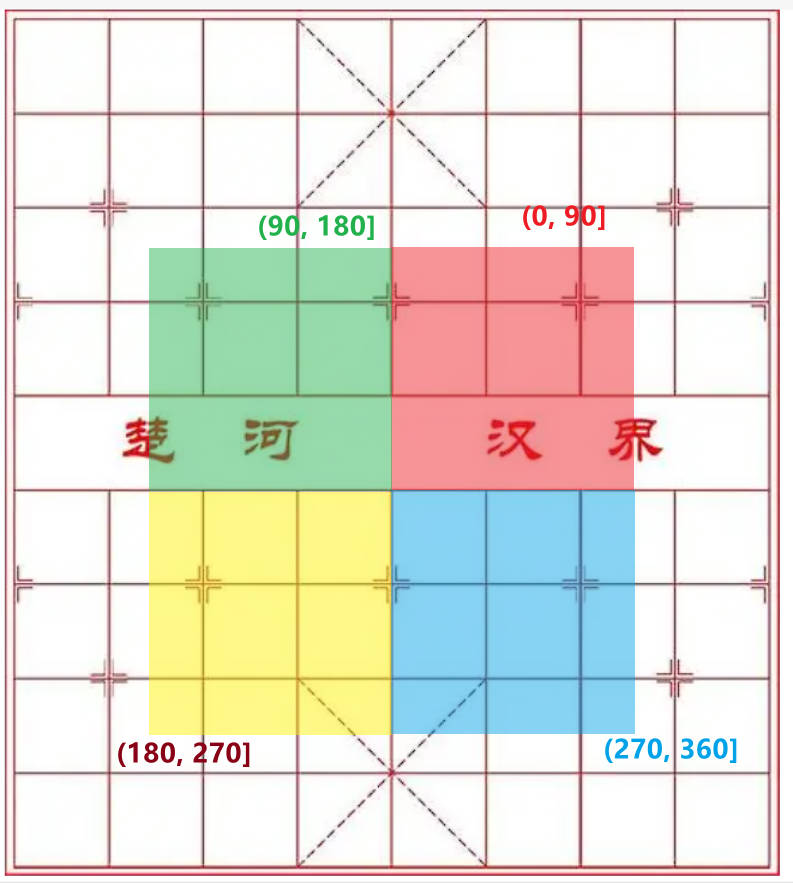
2.计算一下每个象限需要几个方向。
拿第一象限举例:
第一象限肯定要包含以下两个方向
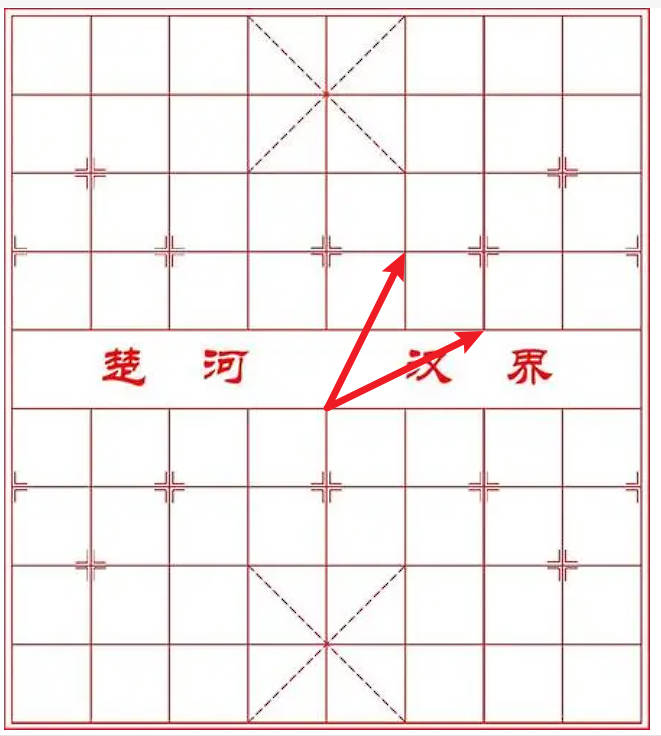
以下两个方向也可能和第一象限有关(其实朝着右下角的那个方向也是可以忽略的,因为象限区间是左闭右开的)
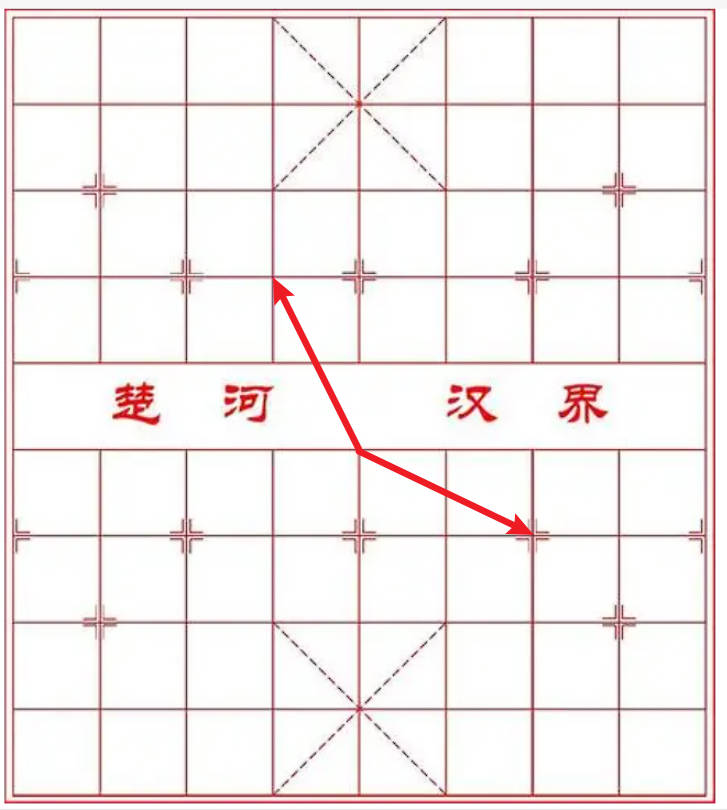
也就是说,我们可以根据当前位置到目标的方向在哪一个象限,来确定我们要搜索的方向。
这样我们就消除了一半的广度。
分析完了,写代码就简单了。
代码如下:
using System; using System.Collections.Generic; internal class Program { public static void Main() { Solution solution = new Solution(); string line = ""; while((line = Console.ReadLine()) != null) { string[] tokens = line.Split(' '); Console.Write("\n"); Console.WriteLine(solution.CalcPathLength( ( int.Parse( tokens[0] ), int.Parse( tokens[1] ) ) ) ); Console.Write("\n"); } Console.ReadKey(); } } public class Solution { //马的8个方向向量 List<(int, int)> direct = new List<(int, int)>() { (2, 1), (1, 2), (-1, 2), (-2, 1), (-2, -1), (-1, -2), (1, -2), (2, -1), }; public int CalcPathLength((int, int) target) { //记录路径长度 int length = 0; //用来存储搜索目标的队列 Queue<(int, int)> bfsQ = new Queue<(int, int)>(); bfsQ.Enqueue((0, 0)); while(bfsQ.Count > 0) { //表示是否找到目标的bool值 bool isFind = false; //BFS模板 int count = bfsQ.Count; while (count-- > 0) { (int, int) curPos = bfsQ.Dequeue(); if(curPos.Item1 == target.Item1 && curPos.Item2 == target.Item2) { isFind = true; break; } (int, int) curDirect = (target.Item1 - curPos.Item1, target.Item2 - curPos.Item2); //将方向分为4个象限,保持左开右闭的原则 //第一象限 if (curDirect.Item1 >= 0 && curDirect.Item2 > 0) { bfsQ.Enqueue(CalcNextPos(curPos, direct[7])); bfsQ.Enqueue(CalcNextPos(curPos, direct[0])); bfsQ.Enqueue(CalcNextPos(curPos, direct[1])); bfsQ.Enqueue(CalcNextPos(curPos, direct[2])); } //第二象限 else if (curDirect.Item1 < 0 && curDirect.Item2 >= 0) { bfsQ.Enqueue(CalcNextPos(curPos, direct[1])); bfsQ.Enqueue(CalcNextPos(curPos, direct[2])); bfsQ.Enqueue(CalcNextPos(curPos, direct[3])); bfsQ.Enqueue(CalcNextPos(curPos, direct[4])); } //第三象限 else if (curDirect.Item1 <= 0 && curDirect.Item2 < 0) { bfsQ.Enqueue(CalcNextPos(curPos, direct[3])); bfsQ.Enqueue(CalcNextPos(curPos, direct[4])); bfsQ.Enqueue(CalcNextPos(curPos, direct[5])); bfsQ.Enqueue(CalcNextPos(curPos, direct[6])); } //第四象限 else { bfsQ.Enqueue(CalcNextPos(curPos, direct[5])); bfsQ.Enqueue(CalcNextPos(curPos, direct[6])); bfsQ.Enqueue(CalcNextPos(curPos, direct[7])); bfsQ.Enqueue(CalcNextPos(curPos, direct[0])); } } //如果找到目标,直接break if (isFind) break; length++; } return length; } //计算马下一步走到的位置 private (int, int) CalcNextPos((int, int) curPos, (int, int) direct) { return (curPos.Item1 + direct.Item1, curPos.Item2 + direct.Item2); } }
C#
3. 王子救公主
敌人是强盗,给定一个数组,这个数组中存储了每一个强盗的力量。
王子有两个属性,一个是体力,一个是体力增长值。
每天开始时,王子的体力会增加体力增长值的数值(体力 += 体力增长值)
王子有两个选项,打强盗和休息。
王子只能打力量不大于王子体力的强盗(体力 >= 强盗力量)
击败强盗后,王子的体力清零,体力增长值 + 1
王子休息后,当天体力保留到第二天。
求王子救出公主最少要几天。
我直接贪心写只过了90%。
我的思路是每次王子都去打当前体力值能击败的最强的强盗。
看牛客网上有大佬说用动态规划或者二进制枚举写。链接在这
